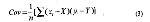Коэффициент ковариации

между двумя переменными х и у, а коэффициент корреляции:

где n — количество наблюдений, xi и yi — значения переменных х и у; Х и Y — средние арифметические значения переменных х и у по ряду наблюдений; σx и σy — средние квадратические отклонения переменных х и у по ряду наблюдений.

Таким образом очевидно, что коэффициент корреляции — это тот же коэффициент ковариации, только нормированный по среднему квадратическому отклонению или, как еще говорят, выраженный в единицах среднего квадратического отклонения переменных. Из этого следуют и "рецепты" по применению в ФА корреляционной или ковариационной матриц:

1) если все переменные выражены в одних и тех же единицах измерения, то нет большого различия, какую из матриц факторизовать;

2) если метрики переменных заметно отличаются (единицы измерения значительно неоднородны и дисперсии переменных заметно отличаются), то целесообразно использовать анализ корреляционной матрицы;

3) ковариационные матрицы предпочтительнее, когда необходимо провести сравнение результатов ФА (факторных структур) в двух различных выборках, полученных в одном и том же исследовании, например, когда требуется оценить повторяемость какого-либо интересного результата.

2. Следующий важнейший этап ФА — собственно факторизация матрицы корреляций (ковариации) или выделение первоначальных (ортогональных) факторов. В настоящее время — это полностью компьютеризованная процедура, которую можно найти во всех современных статистических программах. Одним из первых, кто предложил формально-математическое решение проблемы возможности факторизации корреляционной матрицы, был Л. Терстоун. В матричной форме его известное уравнение выглядит следующим образом (подробнее см.: Я. Окунь, 1974, с. 43-49):

где ||R|| — редуцированная корреляционная матрица;

||F|| — редуцированная матрица факторных нагрузок;

||F’|| — транспонированная матрица факторных нагрузок.