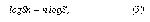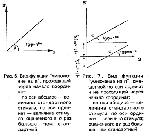
Разделив второе равенство на первое и проведя элементарные преобразования, получим:

Итак, линия "умножения на n" оказывается прямой с наклоном n, но не проходит через начало координат (см. рис. 7).

Построив прямую наилучшего приближения по данным "умножения на n", вычислим аналогично тому, как это делалось в предыдущем пункте А, показатель степени Стивенса. Однако, непрохождение прямой через (0,0) не позволяет ограничиться проделанным: недостаточно знать только α, нужно еще вычислить S0. Прямая "умножения на n" пересекает ось ординат на уровне (1 – n1/α)S0. Разделив эту величину на (1 - n1/α), получим S0.

На рис. 6 и 7 изображена прямая "умножения на n" в предположении, что Z = aSα (рис. 6) и в предположении, что Z = k(Sn – S0)α (рис. 7). На рис.7 также показан случай, когда (1 – n1/α)S0 — величина отрицательная. Если S действительно является "порогом", то независимо от знака этой величины S0 должна быть величиной положительной. Если этого не произойдет, то интерпретация S0 меняется. Функция Z = k(S + r)α (где r > 0) показывает наличие "шума", так что и при нулевом стимуле S0 имеет место ненулевое ощущение Z = krα. Эта разница в интерпретации не влияет на формальный анализ.

3. Простейшая логарифмическая зависимость Z = logS. В этом случае пара равенств, задающих кривую "умножения на n" такова:

Очевидно, что, проведя те же вычисления, как и в предыдущих пунктах, мы получим:

т.е. определенно нелинейную зависимость. Значит, если мы ожидаем логарифмическую, а не степенную зависимость, не следует строить прямых наилучшего приближения.

Если мы все же их построим, то они окажутся "плохими" в смысле приближения к опытным точкам, и самое главное, вычисления по разным n (n = 1/2, 1/3 и 2) дадут нам разные величины а. Выход из затруднения состоит в том, что данные "умножения на n" следует откладывать в двойных логарифмических координатах. Тогда, согласно (2"), наилучшим приближением будет прямая, наклон которой равен коэффициенту фракционирования n (см. рис. 8).