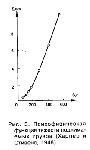
В дальнейшем психофизическая зависимость может использоваться для определения шкальных значений любого стимула, в том числе и такого, который не применяется в опыте, например, лежащего между S’1 и S’2. В самом деле, такому стимулу нельзя приписать однозначно шкальное значение, поскольку к нему нельзя "прийти" от предъявлявшихся в эксперименте стимулов S1 или S2 путем описанной выше процедуры с помощью кривой "деления на n". Можно только утверждать, что его шкальное значение лежит между 1/n и 1. Это утверждение будет справедливо лишь при допущении, что психофизическая зависимость является строго монотонной. Неточность в определении шкального значения, соответствующего этому стимулу, возрастает за счет ошибки при построении психофизической зависимости.

Психофизическая функция, построенная по данным Харпера и Стивенса показана на рис. 3.

Аналитический способ, который дает более точное определение субъективной шкалы, поскольку лишен ошибок, связанных с неточностью проведения графических работ, подробно описан Гилфордом (1954). Здесь приведем только краткую схему аналитического решения, поскольку для тех, кто владеет минимальными навыками регрессионного анализа, с помощью любой современной статистической программы оно не представляет большого труда (СНОСКА: Конкретные методические рекомендации о том, как выполнить эту процедуру с помощью статистической системы "Stadia", будут даны ниже при описании учебного задания). Подобранные в опыте значения стимулов, оцененных как в п раз меньшие (большие), чем стандартные, преобразуются в логарифмы и с помощью метода наименьших квадратов определяется уравнение прямой. Качество подгонки полученной прямой под экспериментальные точки оценивается стандартным образом. Используя это уравнение, можно вычислить любое значение на оси "X" по известному значению на оси "Y" (и наоборот). Естественно, что точность получаемых оценок будет зависеть от качества полученной регрессионной прямой. Находя таким образом нужные значения на оси "X" конструируемой психофизической функции, получают все необходимые точки. После этого, применяя методы регрессионного анализа, определяют вид функции, описывающей психофизическую зависимость. Поскольку психофизические функции, как правило, нелинейны, удобнее представлять результаты на графике и проводить регрессионный анализ в логарифмическом масштабе по оси абсцисс. Если эта функция подчиняется закону Фехнера, то в этом случае она будет прямой. Если же психофизическая функция степенная, то представление ее в виде прямой можно получить только в двойных логарифмических координатах (так называемые log-log-координаты), т.е. введя логарифмический масштаб также и по оси ординат. Таким образом, изображение психофизической функции в виде прямой в логарифмических координатах, является своеобразным "тестом" на ее соответствие одному из основных психофизических законов.