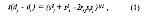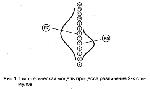
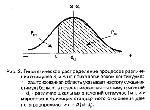
3. В качестве значения i-го стимула на психологической шкале принимается среднее (Si) распределения процессов различения, а дисперсия распределения рассматривается как дисперсия различения (σi).

4. Предъявление одновременно пары стимулов вызывает два процесса различения di и dj. Разность (dj - di) называется различительной разностью. При большом числе предъявлений двух стимулов различительные разности также формируют свое нормальное распределение на психологическом континууме. Поэтому среднее распределение разностей различения (dj - di) будет равно разности средних распределений самих процессов различения — (Sj - Si), а дисперсия распределения различительных разностей равна

где si и sj — дисперсии процессов различения i-гo и j-гo стимулов, соответственно, а гi,j — есть корреляция между мгновенными значениями процессов различения стимулов i и j.

Рассмотрим теперь следующую ситуацию. Пусть наблюдателю предъявляются пары стимулов i и j и от него требуется осуществить суждение, какой из стимулов дальше отстоит от нуля на психологическом континууме (например, более тяжелый или более сложный, или более красивый и т.д.). На рис. 1 показаны гипотетические процессы различения стимулов i и j.

Предполагается, что если различительный процесс для стимула j окажется на психологическом континууме выше, чем для стимула i, т.е. если различительная разность (dj - di) > 0, то последует суждение, что стимул j больше, чем стимул i. И соответственно при (dj - di) < 0 — произойдет обратное суждение.

Однако, если распределения различительных процессов перекрываются, то суждение, что стимул j меньше, чем стимул i может произойти даже тогда, когда величина Sj на психологическом континууме больше, чем величина Si. На рис. 2 показано распределение различительных разностей при большом числе суждений.

Среднее распределения равно различию шкальных величин двух стимулов — (Sj - Si). Это различие можно найти из таблицы областей под единичной нормальной кривой, зная пропорцию суждений стимул j больше, чем стимул i от общего числа суждений по данной паре стимулов (т.е., сделав стандартное преобразование "р → z" ).