| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Новиков А.М., Новиков Д.А. Методология. –– М.: СИНТЕГ. – 663 с.
Стр. 246 Такой вывод вполне соответствует здравому смыслу, и для его получения вряд ли стоило формулировать математическую задачу оптимизации. Однако, если усложнить модель (например, учесть риск или тот факт, что проекты могут требовать фиксированных инвестиций и давать фиксированную отдачу, и т.п.), то задача станет не столь тривиальной и без оптимизационных моделей нельзя будет обойтись (см. примеры в [26, 29]). Например, пусть имеются 100 единиц ресурса и два проекта. У первого проекта отдача на единицу вложенных средств равна 1,8, у второго – 1,4. Вероятность успешного завершения первого проекта равна 0,85, второго – 0,95. Требуется распределить инвестиции между проектами так, чтобы ожидаемый доход был максимален: 1,8×0,85×x1 + 1,4×0,95×x2 ® max, при условии, что расходуется количество ресурса, не большее имеющегося: x1 + x2 £ 100, и ожидаемые потери не должны превышать 9 % от имеющегося ресурса: (1 – 0,85)×x1+ (1 – 0,95)×x2 £ 9. Данная оптимизационная задача (являющаяся задачей линейного программирования [201]) имеет следующее решение: Отметим, что при постановке и решении оптимизационных задач существенное значение имеет выбор критерия эффективности и ограничений. Так, если в рассмотренном выше примере в ограничении на ожидаемые потери заменить 9 % на 11 %, то оптимальным будет совсем другое решение: Мы привели простейший пример задачи оптимизации. Читателей, заинтересованных в более подробном изучении теории оптимизации, отсылаем к [26, 27, 29, 44, 55, 150, 172, 192, 201, 217] и спискам литературы в этих источниках. |
Реклама
|
||
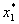 = 40,
= 40, 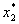 = 60. Значение критерия эффективности при этом равно 141.
= 60. Значение критерия эффективности при этом равно 141.