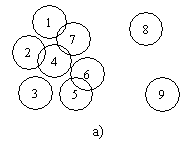
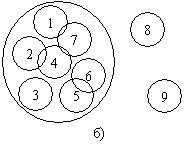
У исследователя, взявшегося за такое обобщающее исследование, появляются многочисленные разнородные и разноаспектные результаты, которые трудно объединить в единое целое.

Начинается длительный поиск – какая же предметная область, какая же формулировка темы, какая концепция могут объединить, собрать воедино все наработанные результаты или, по крайней мере, их бóльшую часть. Ведь нередко бывает, что часть результатов никак не ложится в единое русло и их приходится отбрасывать. В то же время подчас оказывается, что чего-то из необходимых результатов недостает, и исследование следует продолжить. Здесь будет уместно привести такую аналогию из теории множеств (Рис. 6 – диаграммы Эйлера–Венна). Представим себе, что имеются отдельные разрозненные результаты – «множества» – 1, 2, 3, 4 и т.д. (см. Рис. 6а). Они могут частично «перекрывать» друг друга. Задача состоит в том, чтобы найти такое общее множество – объединяющее множество (см. Рис. 6б), которое вберет в себя все или, по крайней мере, большую часть отдельных множеств. Подчас отдельные результаты, не относящиеся к определенной конечной предметной области, приходится отбрасывать (на Рис. 6б – это множества 8 и 9).

Рис. 6. Диаграммы Эйлера-Венна. Нахождение «объединяющего» множества

Как правило, такую объединяющую предметную область можно выявить.

Попробуем описать примерный «алгоритм» этого поиска. Зададимся в самом общем виде вопросом – откуда появляются новые результаты, которые могут стать основой для обобщающего исследования? Представим себе три условные плоскости (см. Рис. 7): плоскость предметных областей; плоскость методов и средств познания – условно назовем их общим названием «технологии» (познания); плоскость результатов.

Рис. 7. Варианты получения новых научных результатов

Новые результаты могут быть получены: