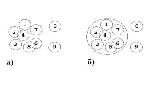
Но поскольку эти полученные многочисленные результаты разнородны, разноаспектны, они трудно объединяются в единое целое. И чаще всего соискатель на этом начальном этапе оформления диссертации пытается сформулировать ее тему в виде традиционно-банальной расплывчатой формулировки типа «Пути совершенствования...» (чего-либо). Это как раз тот этап, когда есть «материал для докторской диссертации», но докторской диссертации нет.

 Начинается длительный поиск – какая же предметная область, какая же формулировка темы, какая концепция может объединить, собрать воедино все наработанные результаты или, по крайней мере, их большую часть. Ведь нередко бывает, что часть результатов никак не ложится в единое русло и их приходится отбрасывать. В то же время подчас оказывается, что чего-то из необходимых результатов недостает и исследование следует продолжить. Здесь будет уместно привести такую аналогию из теории множеств (рис. 1. – диаграммы Эйлера–Венна). Представим себе, что имеются отдельные разрозненные результаты – «множества» – 1, 2, 3, 4 и т.д. (рис. 1а). Они, в том числе, могут частично «перекрывать» друг друга. Задача состоит в том, чтобы найти такое общее множество – объединяющее множество (рис. 1б), которое вберет в себя все или, по крайней мере, большую часть отдельных множеств. Как мы уже говорили, подчас отдельные результаты, не относящиеся к определенной диссертантом конечной предметной области, приходится отбрасывать (на рис. 1б – это множества 8 и 9).

Как правило, такую объединяющую предметную область и, соответственно, обобщающую формулировку, а вслед за этим, соответственно, концепцию и тему диссертации можно выявить. Ведь несмотря на то, что исследователь вел нецеленаправленный поиск, тем не менее он, чаще всего интуитивно, оставался в рамках какой-то вполне определенной предметной области и как правило почти полностью ее охватывал.

Рис.1 Диаграммы Эйлера–Венна. Нахождение «объединяющего» множества

Попробуем описать примерный «алгоритм» этого поиска. Зададимся в самом общем виде вопросом – откуда появляются новые результаты, которые могут стать основой для докторской диссертации? Представим себе три условные плоскости (рис. 2): плоскость предметных областей; плоскость методов и средств познания – условно назовем их общим названием «технологии» (познания); плоскость результатов.