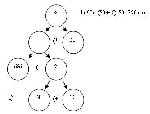
Запись принимает вид (рис.6).

Рис.6

Можно ли узнать это время? (Можно. Есть оба данных: 50 ч и 48 ч.). Каким действием? (Сложением).

Запись принимает вид (рис.7).

Рис.7

1) 686:(50+48)×50=350 (л)

1)

Что осталось узнать? (Сколько горючего израсходовал второй трактор).

Можно это узнать? (Можно).

Почему? (Всего израсходовали 686 л, и первый трактор израсходовал 350 л, значит, остальное горючее израсходовал второй трактор). Запись приобретает вид (рис.4).

Возможен и другой способ нахождения ответа на последний вопрос, он нас тоже устроит. Появляется окончательная запись решения. Письменно дети подсчитывают только то, что не могут сосчитать устно. Наличие схемы разбора в тетради не обязательно, ее можно делать на черновике. Учитель может проконтролировать понимание решения различными способами, как прямыми, так и косвенными (прямые – объяснить устно каждый шаг, написать план решения и т.д.; косвенные – решить похожую задачу, составить обратную и т.д.).

Предложенный способ позволяет экономить время записи решения задач. Кроме того, в процессе данной работы дети овладевают деятельностью схематизации, а затем и моделирования (анализ текста задачи, математизация, преобразование модели, соотнесение полученной модели с задачей). Именно такая деятельность помогает детям глубже проникнуть в суть задачи. При одновременном построении схемы разбора задачи и записи решения виден развернутый план решения задачи и арифметические действия, которые необходимо выполнить. Схема разбора выступает в данной ситуации в двух функциях: абстрактной модели и конкретного отображения содержания, связей и решения задачи.

Выбор приема ознакомления детей с записью решения задачи составлением числового выражения, на наш взгляд, должен осуществляться дифференцированно, в зависимости от состава класса. Можно применять все три приема последовательно. Например, сначала объяснить материал третьим способом, затем, по необходимости, применять первый и второй способы в индивидуальной работе.