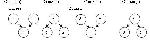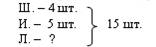
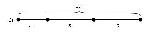
От исходной модели можно перейти непосредственно к схемам решения:

Или

На наш взгляд, последняя схема позволит быстро найти путь к решению задачи.

Многоступенчатость составления краткой записи позволяет ребенку рассмотреть задачу со всех «сторон», позволяет найти различные способы решения задач.

Также можно обучать учеников составлению графов-моделей (схем) задачи (СНОСКА: Подробнее: Белошистая А.В. Прием графического моделирования при обучении решению задач. // Начальная школа. – 1991. - № 4. – С.18 -24), начиная с решения простых задач на нахождение суммы и остатка.

Идея построения граф-схемы задачи основывается на том, что в условии задачи рассматриваются связанные зависимостью элементы. Эти зависимости выражаются отношениями, которые обычно связывают три величины. Такие связанные тройки величин представляют собой либо простую задачу, либо простые задачи, входящие в составную задачу. Они и являются основными компонентами структуры задачи. Схематично каждая из связок представляется в виде своеобразного «треугольника». Структура составной задачи на схеме обычно выглядит как объединение конечного числа таких «треугольников».

Например, рассмотрим задачи «В коробке было 5 карандашей. Миша положил туда еще 2 карандаша. Сколько карандашей стало?» и «В коробке лежало 5 карандашей. 2 карандаша взяли. Сколько карандашей осталось в коробке?».

Разбор задач на нахождение суммы и остатка проведем от данных к вопросу и от вопроса к данным, при этом, обучая детей составлять схемы разбора и решения задачи. В схемах можно использовать также и знаки арифметических действий, что позволяет трансформировать их в план-схему решения задачи.

Схемы (а) и (с), а также (б) и (д) совпадают. Практически по каждой из схем можно составить два числовых выражения со знаком (+) и (–). Поэтому детям можно предложить добавить в схемы знаки арифметических действий, чтобы схема относилась к конкретной задаче.