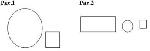
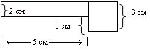
I. Упражнения, иллюстрирующие упорядоченность множества площадей фигур отношением «иметь меньшую площадь».

1. Площадь какой из фигур, изображенных на рисунке 1, меньше? Верно ли, что площадь круга меньше площади квадрата? (Свойство асимметричности отношения «меньше» на множестве площадей геометрических фигур.)

Верно ли, что площадь данного прямоугольника, изображенного на рис.2, меньше площади этого же прямоугольника? (Свойство антирефлексивности отношения «меньше» на множестве площадей геометрических фигур.) Сравните площади фигур.

Наложением фигур друг на друга дети устанавливают, что площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника. Учащиеся убеждаются также, что площадь квадрата меньше площади прямоугольника. Учитель подводит итог этой работы: «Так как площадь квадрата меньше площади круга, а площадь круга меньше площади прямоугольника, то площадь квадрата меньше площади прямоугольника».

II. Упражнения, приводящие к понятию площади фигуры.

1. На сколько квадратных сантиметров площадь квадрата со стороной 3 см меньше площади квадрата со стороной 5 см? (Существование разности площадей.)

III. Упражнения, иллюстрирующие переместительное свойство сложения площадей фигур.

Чему равна площадь фигуры?

Учитель вместе с учащимися составляет выражения:

2-5+3-3 (кв. см) – площадь данной фигуры;

3 • 3 + 2 • 5 (кв. см) – площадь этой же фигуры. В результате вычислений устанавливается, что 2 • 5 + 3 • 3 = 3 • 3 + 2 • 5.

Решение этих задач подтверждает свойство переместительности сложения в множестве площадей фигур.

IV. Упражнения, иллюстрирующие сочетательное свойство сложения площадей фигур.

Определить площадь фигуры различными способами. Одному из способов соответствует выражение (3×3+3×1) + 4×3 (кв. см), другому – 3×3 + (3×1 + 4×3) (кв. см.).

Вычисляя значения этих выражений, учащиеся устанавливают, что сложение величин ассоциативно.