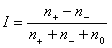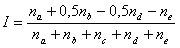Если обозначим через n+ — число «уверенных», n — число «неуверенных», а через n0 — число «нейтральных», то индекс I будет иметь следующий вид:

Какой бы индекс социолог ни использовал, он необходимым образом выясняет свойства этого индекса, т. е. выясняет правила его «поведения». Данный индекс обладает следующими свойствами. Он принимает максимальное значение, равное 1, тогда, когда все респонденты в группе уверены, что найдут работу по специальности. Он принимает минимальное значение, равное —1, тогда, когда все респонденты не уверены, что найдут работу по специальности. Индекс равен нулю, если число «уверенных» равно числу «неуверенных». Положительное значение индекса говорит о том, что уверенных больше, чем неуверенных. И соответственно, отрицательное значение появится в ситуации, когда число неуверенных больше, чем уверенных. Понятно, что в группах с одинаковой разницей (отличной от нуля) между числом уверенных и неуверенных (это называется абсолютной разницей в отличие от относительной), значение индекса будет больше в той группе, где меньше нейтральных ответов.

А теперь, опираясь на те же рассуждения, можно предложить аналогичный индекс и для случая пяти градаций. Обозначим через na — число уверенных студентов, nb — число скорее уверенных, чем нет, nc — число нейтральных, nd — число не очень уверенных и ne — число скорее неуверенных. Тогда можно предложить индекс следующего вида:

Если в предыдущей формуле все коэффициенты при разных n (частотах) были равны единице, то в этой формуле появились коэффициенты разные (1 и 0,5). Это означает, что отдельно взятая градация вносит разный вклад, разную долю в значение индекса. Коэффициент, равный 0,5 перед nb и nd вводится для того, чтобы сделать равноправными «не очень уверенных» и «скорее неуверенных». Это во-первых. Во-вторых, вклад тех, кто «не очень», в два раза меньше, чем вклад тех, кто «очень». И наконец, рассмотрим ситуацию, когда в группе нет респондентов уверенных, нейтральных, не очень уверенных, совсем неуверенных, а все респонденты скорее уверены, чем нет. Тогда значение индекса будет равно 0,5. Аналогичные рассуждения можно продолжить для выяснения всех остальных свойств индекса.