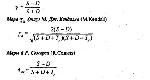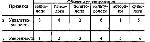
Приведем примеры нескольких коэффициентов, а затем поясним их содержательный смысл.

Мера g (гамма) Л. Гудмена и Е. Краскала (L. Goodman, E.Kraskal)

Первая из этих мер в работе [8, с. 135], обозначена как «g Гудмана». Эти меры удачно описаны в работе [1, с. 37—40]. Вы, конечно, обратили внимание, что у всех приведенных мер один и тот же числитель, а знаменатели различны. Прежде всего рассмотрим числитель, ибо он несет в себе основное содержание коэффициентов, В таблице 3.5.4 представлены два ранжированных ряда. Объекты ранжирования ¾ будущие профессии. Они приведены в таблице для удобства в том порядке, в котором их ранги во втором ряду возрастают, т. е. в порядке убывания степени уверенности. Число рангов равно числу объектов, связанных рангов (одинаковых) в наших рядах не наблюдается.

Таблица 3.5.4. Примеры двух ранжированных рядов

Из этой таблицы видим, что политологи в первом ряду имеют ранг 2, а во втором ¾ ранг 3, а историки в первом ряду ¾ ранг 1, во втором ¾ ранг 5. Для того чтобы оценить степень согласованности наших, грубо говоря, «ранжировок», можно применить тот же прием, который был применен при вычислении меры качественной вариации. Образуем из наших шести объектов различные пары. Таких пар будет 6x5/2=15. Возьмем отдельную пару объектов. Ранги, соответствующие первому объекту, обозначим (i1, j1), а второму ¾ (i2, j2). Эти ранги могут находиться в различных отношениях. Возможна одна из двух ситуаций, каждая из которых включает два возможных соотношения между рангами (1а, 16, 2а, 26).

В первой ситуации ранги как бы согласованы, а во втором не согласованы. Подсчитаем, для скольких пар из 15-ти наблюдается согласованность, и обозначим число таких пар через S. Затем подсчитаем, для скольких пар наблюдается несогласованность, и обозначим число таких пар через D. В числителе всех приведенных выше мер стоит как раз разница между числом согласованных и несогласованных пар объектов. Для примера наших ранжированных рядов величина (S-D) равна: