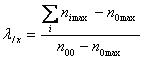niшах ¾ максимальная частота в i-й строке:

nотах ¾ максимальная частота среди маргинальных частот по столбцам.

Эта формула была бы понятнее, если вместо частот использовать частости (доли), интерпретируемые как вероятности [11, с. 126]. Такую формулу мы не будем приводить, чтобы не пугать излишними формулами. Отметим лишь, что в литературе приводится как формула, записанная через абсолютные частоты, так и через частости. Кроме того, фамилия Гуттмана тоже приводится по-разному. Например, Гудман в работе 8, с. 131. Это не так уж важно.

Для того чтобы пояснить содержательный смысл этой меры, этого коэффициента, ниже приводится та же таблица сопряженности, с которой мы постоянно работаем для изучения взаимосвязи между «будущей профессией студента» (признак X) и «удовлетворенностью учебой» (признак У). Таблица 3.5.1 содержит те же частоты, что и таблица 3.3.1, за исключением обозначений самих частот. В нее добавлен новый столбец ¾ последний с максимальными частотами по всем строкам, включая строку с маргинальными частотами по столбцам. Они нам необходимы для вычисления коэффициента lу/х Гуттмана.

Чему же равен коэффициент в нашем случае? Он рассчитывается очень просто.

Даже по тому, как вычисляется коэффициент, видно, что он позволяет определять, существуют ли в строках модальные группы, т. е. есть ли в каждой профессиональной группе ярко выраженная, часто встречаемая «степень удовлетворенности учебой». Судя по нашей таблице, таких групп практически нет, что и подтверждается маленьким значением коэффициента. Какими же свойствами обладает этот коэффициент?

1. Он изменяется от нуля до единицы.

2. Он равен единице только в одном случае, когда в каждой профессиональной группе все студенты имеют одинаковую степень удовлетворенности учебой и при этом в каждой отличную от другой. Если бы наша таблица сопряженности при тех же маргинальных частотах имела бы такой вид, как это представлено в таблице .3.5.2, коэффициент был бы равен 0,86.