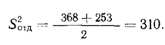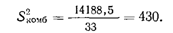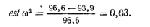| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Готтсданкер Р. Основы психологического эксперимента: Учеб. пособие. Пер. с англ. —— М.: Изд-во Моск. ун-та, 1982. — 464 с.
Стр. 152
В статистическом приложении к главе 3 мы вычислили ∑х2 для условия А (свет) и условия Б (тон):
Используем эти величины для нахождения S2отд. Согласно Хейсу (с. 418), среднее по S2A и S2Б дает величину S2отд при допущении равенства «истинных» дисперсий двух наборов:
Поэтому
Такое же вычисление производится для комбинированного распределения:
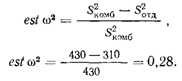
Подставляя эти величины в формулу 4.2, получаем
Это показывает сильную связь между независимой и зависимой переменными. Даже значение 0,20 уже достаточно существенно. Значение никогда не может превысить 1; однако эта величина достигается редко. В то же время вычисление для эксперимента с испанским языком дает Это очень слабая связь между независимой и зависимой переменными. Применения Ω2 Обратите внимание, что для S2отд необходимо допускать равенство истинных дисперсий для двух условий. В эксперименте по измерению времени реакции это допущение было приемлемым, поскольку дисперсии для двух условий довольно близки по величине. Это справедливо и для эксперимента с испанским языком. Однако для эксперимента с информацией о ценах (см. табл. 4.1) условие В давало значительно меньшее стандартное отклонение (особенно для времени выбора покупки), чем другие условия. Три дисперсии (квадраты стандартных отклонений) были равны 100, 92 и 1,2 для условий А, Б и В. При столь значительном различии прямого способа вычисления ω2 нет. И здесь дело не в том, что число условий равно трем, а не двум. Если значения дисперсии близки, то величина ω2 может быть вычислена для любого числа условий с использованием S2отд как среднего значения для всех условий. Приводившаяся процедура вычисления ω2 может быть использована как для интраиндивидуальных, так и для межгрупповых данных. Дисперсия — это то, что относится к пробам, а не к испытуемым. |
Реклама
|
||
 (4.3)
(4.3)
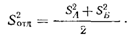 (4.4)
(4.4)