| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Готтсданкер Р. Основы психологического эксперимента: Учеб. пособие. Пер. с англ. —— М.: Изд-во Моск. ун-та, 1982. — 464 с.
Стр. 151 Рис. 4.5. Объединенное частотное распределение средних значений Семени реакции. Ось абсцисс — средние значения времени реакции (в мс). Ось ординат — частота Наше вычисление с использованием данных по выборке испытуемых дает оценку ω2. Мы будем называть ее est ω2. Давайте построим новый график результатов эксперимента по измерению времени реакции. Однако теперь мы не будем делать различий между тем, какое из двух условий — А (свет) или Б (тон) — было использовано. Как видно на рис. 4.5, это комбинированное распределение несколько более растянуто, чем каждое из отдельных распределений для света и тона. Чем больше исходные распределения отличаются друг от друга, тем больше будет растянуто комбинированное распределение. Если бы мы смогли провести бесконечный эксперимент и при этом получили бы распределения, показанные на рис. 4.4 и 4.5, мы могли бы вычислить ω2 прямо из параметра σ̅2X следующим образом:
Однако поскольку наши данные получены только по одной выборке испытуемых, а не в бесконечном эксперименте, мы должны оценивать ω2 по статистике S2X:
Квадрат стандартного отклонения распределения называется дисперсией. Числитель этой формулы дает разность между дисперсиями комбинированного распределения и отдельного распределения, в нашем случае любого из условий А или Б. Делением этой разности на дисперсию комбинированного распределения мы придаем ей форму пропорции. Она отвечает на вопрос, на какую часть уменьшается дисперсия показателей при переходе от комбинированного распределения к отдельному. Производя вычисления, нет необходимости сначала вычислять SX и затем возводить его в квадрат, чтобы получить S2X. Вспомните (из формулы 2.2):
Поэтому |
Реклама
|
||
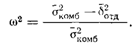 (4.1)
(4.1)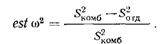 (4.2)
(4.2)