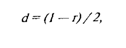Для первичного представления данных используются другие графические формы: диаграммы, гистограммы и полигоны распределения, а также различные графики.

Первичным способом представления данных является изображение распределения. Для отображения распределения значений измеряемой переменной на выборке используют гистограммы и полигоны распределения. Часто для наглядности распределение показателя в экспериментальной и контрольной группах изображают на одном рисунке.

Гистограмма — это "столбчатая" диаграмма частотного распределения признака на выборке. Используется декартова система координат. При построении гистрограмм на оси абсцисс откладывают значения измеряемой величины, а на оси ординат — частоты или относительные частоты встречаемости данного диапазона величины в выборке. Если на гистрограмме отображены относительные частоты, то площадь всех столбиков равна 1.

В полигоне распределения количество испытуемых, имеющих данную величину признака (или попавших в определенный интервал величины), обозначают точкой с координатами: Х — градация признака, Y — частота (количество людей) конкретной градации или относительная частота (отнесение количества людей с этой градацией признака ко всей выборке). Точки соединяются отрезками прямой. Перед тем, как строить полигон распределения, или гистограмму, исследователь должен разбить диапазон измеряемой величины, если признак дан в шкале интервалов или отношений, на равные отрезки. Рекомендуют использовать не менее 5, но не более 10 градаций. В случае использования номинальной или порядковой шкалы такой проблемы не возникает.

где d — расстояние, r — корреляция.

Расстояния отражают сходства — различия признаков. В этом случае от топологического описания мы переходим к метрическому, поскольку расстояния между вершинами графа (свойствами) становятся пропорциональными величинам корреляций с учетом знака: при r=- 1 расстояние максимально: d = 1, при r = 1 расстояние минимально: d==0.