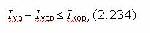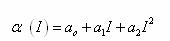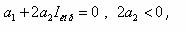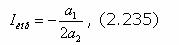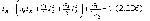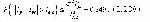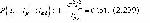Для выявления этой сущности сформулируем закон функционирования системы обучения в установившемся режиме ( 2.225, 2.227) на основе разработанных имитационных моделей функции обученности (2.232) и функции усвоения (2.233):

где Iкор - количество информации корректуры, которое гарантированно усваивается обучаемым с первого ее предъявления.

В соответствии с видом имитационной модели (2.232) функции обучаемости сформулированное при обосновании закона обучения требование a(Iкор)=1 наиболее полно выполняется в точке, где модель (2.232) имеет свой максимум. Имитационная модель

в соответствии с условиями существования максимума непрерывной функции имеет максимальное значение в точке Iкор,где

откуда максимально возможное количество информации корректуры, которое гарантированно может быть усвоено данным обучаемым, определяется как

при 2а2<0

Тогда с учетом (2.232) закон управления обучением (2.234) можно представить в виде:

Решение уравнения (2.236) и определяет то максимально возможное количество Iуо семантической информации об изучаемом УЭ, которое может быть выдано обучаемому в процессе реализации одного обучающего воздействия (цикле обращения учебной информации) и потребует не более одной корректуры его учебной деятельности.

Рассмотрим применение закона (2.236) в отношении обучаемого, данные которого представлены в таблицах 2.3.1, 2.3.3, 2.3.5. В соответствии с данными, представленными в таблице 2.3.5 параметры его полиномиальной модели обучаемости определены в виде:

a0=0.890560, a1=0.000316, a2=-0.0000014, s²=0.0866.

Решая (2.236) с данными параметрами, имеем:

Iкор=158 бит ; Iуо=494.77 бит. (2.237)

Если бы аппроксимирующая функцию обучаемости полиномиальная модель не имела погрешностей, то решение (2.237) было бы верным. Однако, сама модель имеет погрешности, характеризуемые дисперсией s²=0.0866 (s=0.2943). В связи с этим оценим вероятность необходимости корректуры превышающей Iкор = 158 бит для Iуо = 494.77 бит на основании неравенства Чебышева:

В свою очередь вероятность выдачи обучаемому информации меньшей Iкор составит всего

Таким образом, погрешности в определении параметров аппроксимирующей модели определяют высокую оценку Р = 0.849 вероятности необходимости выдачи обучаемому информации корректуры, превышающей ее значение Iкор = 158 бит, т.е. вероятность необходимости неоднократной корректуры деятельности обучаемого. Такая необходимость фактически и имела место у рассматриваемого обучаемого по задаче, имеющей трудоемкость Iэт = 502.11 бит, практически совпадающую с оптимальной оценкой Iуо = 494.77 бит (см.табл.2.3.1, задача 3).