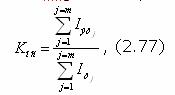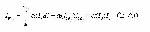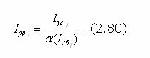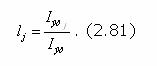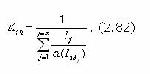где Iпj - количество семантической информации об УОj, предоставляемой обучаемому в процессе реализации алгоритма обучающего воздействия.

В соответствии с критерием (2.62) выбора способа обучения и с учетом aj=1 в рассматриваемом случае:

- Iпj=Iэтj - для обучающих воздействий 2 типа;

- Iпj=2Iэтj - для обучающих воздействий 1 типа.

Тогда предел эффективности функционирования обучающей системы при беспредельно делимом УЭ определяется только параметрами функционирования самой системы:

- Кос=1, если обучающая система использует обучающие воздействия 2 типа (проблемный метод обучения, формирование 3 типа ООД);

- Kос=0.5, если обучающая система использует обучающие воздействия 1 типа (развертывание перед обучаемым фрагмента его учебной деятельности) с полной проверкой качества усвоения УОj обучаемым.

2 случай. В реальном процессе обучения имеется определенное множество {Ri} вариантов стратегий изучения УЭ, обладающих свойством (2.57). Пусть на указанном множестве определена эффективная стратегия Ri, в которой

("УОj(УОj ÎУЭ, aj)). (2.78)

В соответствии с принятой гипотезой деятельность обучаемого подчиняется (2.53,2.54), и (2.74) также имеет вид (2.77). В рассматриваемом случае для определения в (2.77) значений Iпj необходимо сначала оценить Iпрj. В соответствии с (2.54) имеем:

С учетом того, что семантическая информация Iо представляет собой сведения, необходимые обучаемому для начала изучения УОj и Iпрj>>Iо, вторым членом a(I0)I0 в (2.79) можно пренебречь. Тогда из (2.79) имеем:

В соответствии с критерием (2.62) в идеально функционирующей системе Iпj=Iпрj. Введем параметр lj веса УОj (Slj=1):

Тогда с учетом (2.80, 2.81) показатель Кос в (2.77) примет вид:

Таким образом, если деление изучаемого УЭ на УО имеет ограничения и свойство обучаемости обучаемого в отношении хотя бы одного УО меньше единицы (aпрj<1), то предел эффективности обучающей системы имеет следующие ограничения:

- Кос < 1, если обучающая система использует обучающие воздействия 2 типа;

- Кос < 0.5, если обучающая система использует обучающие воздействия 1 типа.

Для ориентации в степени снижения эффективности функционирования обучающей системы в условиях ограничений по делению УЭ на УОj рассмотрим следующий пример, взятый из практики обучения. Для изучения способа решения родовой задачи "Расхождение с одиночной целью в различных условиях обстановки" для обучаемого разработана дидактическая стратегия, предполагающая деление этого УЭ на четыре УО. Данные, характеризующие обучаемого и УЭ, приведены в таблице 2.1.6.