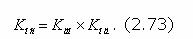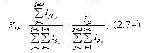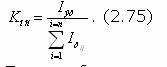Выше были обоснованы показатели эффективности деятельности обучения (2.64-2.66) и обучающей деятельности (2.70-2.72) обучающего. Совокупность данных деятельностей представляет собой процесс функционирования обучающей системы (деятельность обучающего), а указанные выше показатели эффективности образуют полный неизбыточный набор для оценки эффективности функционирования обучающей системы (АОС, обучающего, КОС автономно). Все рассматриваемые показатели эффективности (2.65, 2.66, 2.71, 2.72) удовлетворяют условиям (2.27, 2.28) существования и непрерывности, условиям независимости по предпочтению и приращению, являются показателями "чем больше, тем лучше". Значит, соответствующий им критерий эффективности функционирования обучающей системы (Кос) как их интегральный показатель можно представить в мультипликативной форме (2.33):

Подставляя (2.65, 2.71) в (2.73), для процесса реализации определенной стратегии изучения УЭ имеем:

а в цикле обучения (дидактическом цикле):

Таким образом, эффективность функционирования обучающей системы (АОС, обучающего, КОС автономно) определяется соотношением семантической информации (Iэт), содержащейся в эталонной (нормативной) модели УЭ (УО) с тем фактическим избыточным количеством семантической информации об УЭ (УО), которая была выдана обучаемому для достижения заданного качества усвоения УЭ (УО).

Определим предел эффективности функционирования обучающей системы в отношении конкретного обучаемого на основе гипотез (2.53, 2.54), сформулированных в отношении учебной деятельности обучаемого. Данный предел эффективности функционирования обучающей системы наступает при максимально возможном проявлении у обучаемого свойства обучаемости, т.е. при соответствии его обучаемости кривой (2.53) и изменении качества усвоения УЭ (УО) в соответствии с (2.54), что возможно в условиях "идеальной", т.е. предельно эффективной деятельности обучающего.

Рассмотрим два случая:

- при беспредельно делимом УЭ;

- при УЭ, деление которого на УО имеет ограничения.

1 случай. При беспредельно делимом УЭ, возникает возможность разработки оптимальной дидактической стратегии его изучения, т.е. такой стратегии, в которой

("УОj(УОj Î УЭ, aj=1)), (2.76)

где aj - свойство обучаемости данного обучаемого в отношении УОj.

Другими словами, при беспредельно делимом УЭ возникает возможность его деления на определенное количество УОj такой трудоемкости Iэтj, которая обеспечивает их полное усвоение обучаемым с первого предъявления или проявление максимально возможного (aj=1) свойства обучаемости в отношении этого УОj. Тогда (2.74) примет вид: