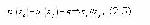| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Печников А.Н. Теоретические основы психолого-педагогического проектирования автоматизированных обучающих систем. -- Петродворец: ВВМУРЭ им. А.С.Попова, 1995. - 322 с.
Стр. 224 В теории эффективности систем цель А считается количественно измеримой на множестве сравниваемых систем S, если на S существует вещественная функция U(S) сохраняющая упорядочение. При этом определяется условие сохранения упорядочения: для любых si, sj Î S, где символ Û означает: "тогда и только тогда, когда". Если измеримые цели позволяют выделить лучшую систему so только непосредственным анализом установленных на множестве S отношений (2.1) предпочтительности, то для количественно измеряемых целей существует и другой подход, при котором so ищется как система, обеспечивающая для siÎS в зависимости от формулировок правой части выражения (2.2). На основе (2.1-2.3) в теории эффективности формально определяется четкое, однозначное и, главное, конструктивное понятие критерия эффективности, приведенное ниже в формулировке В.И. Николаева [83, с.149]. Пусть ЛПР на множестве сравниваемых систем задал бинарное отношение R ( позволяющая вычислить для каждого e > 0 вероятность p истинности утверждения для всех si,sjÎS, не убывает по e. Тогда U(S) есть критерий, характеризующий соответствие систем si Î S цели А. С учетом центральной роли в данном определении функции (2.4) необходимо отметить два подхода к ее определению. Оба эти подхода основаны на обработке информации, полученной от ЛПР, но различаются видом этой информации. Первый подход требует информации, которую можно непосредственно использовать для построения функции (2.4). Для чего в области значений e выделяют множество точек {ei} и предлагают ЛПР указать для каждой из них pi - вероятность того, что siRsj в ситуации, когда о системах известно только одно: u(si) - u(sj)=ei. Затем по полученным данным аппроксимируют искомую функцию (2.4). Второй подход целесообразно использовать в тех случаях, когда ЛПР затрудняется определить величину pi для данного значения ei. Это означает, что задаваемые ЛПР вопросы слишком сложные и их необходимо упростить. Последнее можно сделать, если считать pi случайной величиной, распределенной на интервале [0,1]. Квантили распределения p(pi £ x) задаются ЛПР. Теперь ЛПР не надо определять конкретные значения pi случайной величиной, распределенной на интервале [0,1], а достаточно указать равновероятные интервалы, в которых может оказаться величина pi. По квантилям находится само распределение p(pi £ x), а также его математическое ожидание, которое и принимается в качестве m(e). Процедура определения m(e) по квантилям носит итерационный характер и сравнительно продолжительна, подробное ее описание можно найти в [83]. |
Реклама
|
||
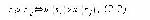
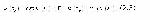
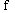 или
или 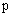 ) и вещественную функцию U(S), значения которой для всех siÎS определены так, что функция
) и вещественную функцию U(S), значения которой для всех siÎS определены так, что функция