| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Морев И. А. Образовательные информационные технологии. Часть 2. Педагогические измерения: Учебное пособие. –– Владивосток: Изд-во Дальневост. ун-та, 2004. – 174 с.
Стр. 116 Задание (задания) выполнено неверно (-1 балл); Решение (задания) содержит погрешность (от -1 до +1 баллов). Не обсуждая достоинства разных шкал, примем за интервал возможных значений rs отрезок от -1 до +1. Полный результат прохождения теста выразится строкой чисел или вектором рейтинга
где n – количество субтестов в тесте, Можно попытаться представить, как плотно заполнен куб результатов. Пусть субтестов будет всего два. Тогда куб результатов будет двумерным и превратится во внутреннюю часть единичного квадрата. В зависимости от выбранного теста, выбранной группы участников и их мотивации, разные области квадрата будут заполнены с разной плотностью. Например, совсем мало результатов окажется вблизи «идеального» результата; очень много результатов может сконцентрироваться в области «наиболее вероятного» результата, который можно получить методом «случайного тыка», и т.д. Теперь, после рассмотрения этого наглядного примера, можно по-другому взглянуть и на задачу процедуры тестирования. Она состоит в том, чтобы, после проведения тестирования, точки-результаты учащихся оказались сгруппированными, распределенными внутри нескольких (немногих) малых областей внутри куба результатов. Учащихся, чьи результаты попали в одну такую область, будут считаться близкими по уровню (качеству) знаний и получат одинаковые оценки. Оси координат в рассматриваемом пространстве результатов лучше представить перпендикулярными друг другу, а соответствующие им единицы измерений – неравными. Хотя, некоторые авторы считают, что более наглядно будет, если представить оси координат наклонными, а неравенство единиц измерений выразить через величины синусов и косинусов углов взаимного наклона осей координат. Принятие одного из этих представлений – дело вкуса. Когда математик слышит о четырехмерных вещах, |
Реклама
|
||
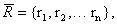 (2)
(2)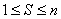 . Поскольку абсолютные значения rs, согласно (1), могут принимать значения от нуля до единицы, вектор
. Поскольку абсолютные значения rs, согласно (1), могут принимать значения от нуля до единицы, вектор 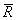 указывает только точки внутри куба или части куба в n-мерном пространстве результатов субтестов. Назовем это пространство пространством результатов. Точку, которую указал вектор рейтинга, будем называть результатом, а куб – область нахождения всех возможных результатов – кубом результатов.
указывает только точки внутри куба или части куба в n-мерном пространстве результатов субтестов. Назовем это пространство пространством результатов. Точку, которую указал вектор рейтинга, будем называть результатом, а куб – область нахождения всех возможных результатов – кубом результатов.