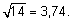| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Валеев Г.Х. Методология и методы психолого-педагогических исследований: Учебное пособие для студентов 3–5-х курсов педагогических вузов по специальности «031000 – Педагогика и психология».–– Стерлитамак: Стерлитамак. гос. пед. ин-т, 2002.– 134 с.
Стр. 79 § 4. Разброс данных вокруг среднегоРазброс полученных данных в положительную и отрицательную сторону от средней величины обозначается буквой d, а вычисляется через отклонение каждого значения от средней ( Вычисление среднего отклонения проводится следующим образом. Собрав все данные и расположив их в ряд– 3, 5, 6, 9, 11, 14,– находят среднюю арифметическую выборки:
Затем вычисляют отклонения каждого значения от средней и суммируют их: -5 -3 -2 +1 +3 +6 (3-8) + (5-8) + (6-8) + (9-8) + (11-8) + (14-8). Но во избежание взаимоуничтожения положительных и отрицательных значений в процессе суммирования общепринято прежде возводить все значения в квадрат, а затем делить всю сумму квадратов на число данных. В нашем примере это выглядит следующим образом: В результате такого расчета получают так называемую дисперсию. Формула для вычисления дисперсии, таким образом, следующая:
После этого из дисперсии извлекается квадратный корень. При этом получается так называемое стандартное отклонение: Стандартное отклонение = В данном примере стандартное отклонение равно Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не , а n –1. Стандартное отклонение обозначается греческой буквой s (сигма):
Стандартное отклонение показывает, насколько далеко от средней разбросаны результаты в положительную и отрицательную стороны. Укладывается ли этот разброс результатов в стандартное отклонение, которое равно 68% популяции. |
Реклама
|
||
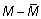 ), затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Если эта средняя невелика, то это свидетельствует в пользу того, что данные больше сконцентрированы относительно их среднего значения и выборка более однородна.
), затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Если эта средняя невелика, то это свидетельствует в пользу того, что данные больше сконцентрированы относительно их среднего значения и выборка более однородна.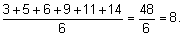

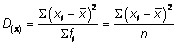 .
.