| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Валеев Г.Х. Методология и методы психолого-педагогических исследований: Учебное пособие для студентов 3–5-х курсов педагогических вузов по специальности «031000 – Педагогика и психология».–– Стерлитамак: Стерлитамак. гос. пед. ин-т, 2002.– 134 с.
Стр. 78 Совокупность характеризуется посредством среднего арифметического в том случае, если распределение параметров расположено симметрично по отношению к середине. При асимметричном распределении или многовершинном полигоне частот среднее арифметическое не подходит для описания совокупности. В таких случаях для характеристики совокупности лучше пользоваться модой. Итак, центральная тенденция распределения частот чаще всего выражается в трех измеряемых средних величинах. Это мода (Mo), медиана (Me) и среднее арифметическое Следует отметить, что каждая мера центральной тенденции числовых рядов измерений и оценки знаний обладает характеристиками, которые ценны в определенных условиях. В малых совокупностях чисел мода, как правило, нестабильна. Например, для совокупности 2, 2, 2, 3, 4, 4 мода равна 2, но если одну из оценок 2 заменить оценкой 4, то мода станет равной 4. Медиана более стабильна. На нее не влияют «большие» и «малые» оценки. Например, для больших совокупностей оценок медиана не изменится, если число минимальных или максимальных оценок резко изменится. Так, например, совокупности 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5 и 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5 имеют одинаковые медианы (Me = 3,5). На величину среднего влияет изменение каждого значения оценки. Для многих числовых совокупностей педагогических измерений мода близка к двум другим мерам – медиане и среднему. Медиана занимает промежуточное положение между модой и средним. Некоторые совокупности результатов педагогических измерений просто не имеют центральной тенденции. Это наблюдается для многомодальных совокупностей оценок (имеющих две и более моды). Например, для совокупностей оценок 2, 2, 2, 2, 2, 4, 4, 4, 4, 4 среднее и мода равна трем, несмотря на то, что даже не существует учащегося с такой оценкой. Ни среднее, ни медиана не в состоянии дать правильного представления об успеваемости этой группы. Более правильное представление об успеваемости этой группы дает словесное описание: «50% в группе имеют оценки «2», а остальные – хорошие». Последнее на языке статистики может быть выражено так: гистограмма бимодальна, т.е. имеет две моды, одна равна 2, другая – 4. |
Реклама
|
||
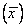 . При нормальном распределении эти три показателя центральной тенденции более-менее совпадают, а при асимметричном распределении получают различное значение.
. При нормальном распределении эти три показателя центральной тенденции более-менее совпадают, а при асимметричном распределении получают различное значение.