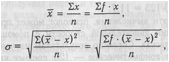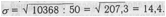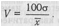В заголовках 5-го и 8-го столбцов указывается, насколько часто встречается та или другая величина. Частота обозначается буквой / (от английского слова frequency).

Включение буквы /, означающей, насколько часто встречалась та или другая величина, ничего не изменяет в формулах среднего арифметического и среднего квадратического отклонения.

Поэтому формулы

вполне тождественны.

Остается показать, как вычисляются по формулам сред16 нее арифметическое и среднее квадратическое отклонение. 12 Обратимся к величинам, полученным в таблице: 8

х = 6150 : 50 = 123.

При составлении таблицы это 4 число было заранее вычислено, без него нельзя было бы получить числовые значения 6, 7, 8-го столбцов таблицы.

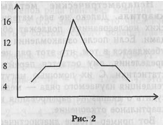
При обработке изучаемого ряда оказалось возможным применение параметрического метода, так как визуально в этом ряду распределение численностей приближается к нормальному. Это подтверждается и графиком (рис. 2, с. 251).

Нормальное распределение обладает некоторыми весьма полезными для исследователя свойствами. Так, в границах F ±ст находится примерно 68% всего ряда или всей выборки, в границах х ±2а — примерно 95%, а в границах F ±3а — 97,7% выборки. В практике исследований часто берут границы — х~ ±2/За. В этих границах при нормальном распределении будут находиться 50% выборки; распределение это симметрично, поэтому 25% окажутся ниже, а 25% выше границ Y ±2/Зст. Все эти расчеты не требуют никакой дополнительной проверки при условии, что изучаемый ряд имеет нормальное распределение, а число элементов в нем велико, порядка нескольких сотен или тысяч. Для рядов, которые распределены нормально или имеют распределение, мало отличающееся от нормального, вычисляется коэффициент вариации по такой формуле:

В примере, который был рассмотрен выше,

V= (10(М4,4)/123 = 11,7.

Выполнив все эти вычисления, психолог может представить информацию об изучении двигательной скорости с помощью примененной методики в 6-х классах. Согласно результатам изучения в 6-х классах получены: среднее арифметическое — 123; среднее квадратическое отклонение — 14,4; коэффициент вариативности — 11,7.