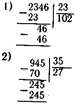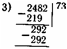27x1=27 — это число меньше 81.

27x2=54 — это число меньше 81.

27x3=81 — получилось число, равное делимому, значит, нал в частном взять по 3. Все промежуточные действия умножени для отыскания нужной цифры частного необходимо производить > тетради. Запись решения примера выглядит так:

Далее последовательно рассматривается деление трех-, четы рех-, пятии шестизначных чисел на двузначное число.

При решении всех этих примеров необходимо учитывать, что отделяемые две цифры делимого составляют число, которое либо равно, либо больше делителя, и только после этого рассматрива ются случаи, когда это число меньше делителя, и в этих случаях требуется отделить три цифры делимого.

Наиболее успевающие по математике учащиеся постепенно сокращают число проб на умножение; умножение делителя на 1 они не записывают, некоторые устно умножают делитель на 2, а то я на 3, и начинают умножать на 4 и 5 и т. д. 240

Естественно, что сильным учащимся следует показать прием мкругления делимого и делителя.

Например, рассматривается деление трехзначных чисел на дву-япачное число при однозначном частном и, например: 465:93. Рассуждения проводим так: «Делитель заменяем круглым числом. ;->то число 90, или 9 десятков. В делимом тоже отделяем десятки, их 46. Делим 46 на 9. В частном берем 5. Проверяем, умножая <)3х5. В данном случае 5 подходит».

Рассматриваются и случаи деления с остатком.

Вслед за делением с остатком рассматривается деление трехзначного числа на двузначное, когда в частном получается двузначное число. Вначале в делимом подбираются такие числа, в которых первое неполное делимое состояло бы из двух цифр, а делитель состоял из цифр, не превышающих 5. «При выполнении деления делитель заменяем наименьшим круглым числом 20. В делимом отделяем две цифры. Первое неполное делимое — 80 десятков. В частном будет двузначное число. 80 делим на 20, будет по 4, но по четыре брать нельзя, так как 23x4=92. Берем по 3. Проверяем: 23x3=69, 80—69=11. Остаток меньше делителя. Значит, первую цифру подобрали правильно. 115 делим на 20. Берем первые две цифры делимого (11) и первую цифру делителя (2), 11 делим на 2. Берем по 5. Проверяем: 23x5=115. Вычитаем. Остатка нет. Значит, 5 подобрали правильно. Частное 35. Проверим умножением: 35x23=805». После этого рассматриваются случаи деления четырехзначного числа на двузначное.