Но в прогнозировании такой системы есть еще весьма существенные недостатки.

При небольшом N система будет очень «доверчивой» в своем прогнозе; влияние на прогноз случайного, но недавно встретившегося события будет значительным; модель будет быстро менять прогноз даже под влиянием случайных изменений среды.

При слишком большом N модель окажется слишком «косной» в своем прогнозе, недостаточно чуткой к изменениям вероятностной характеристики среды.

При N, равном числу всех карточек в ящике (т. е. если модель обладает «бесконечно большой» памятью — в пределах всей ее «жизни»), вероятностный прогноз (как уже говорилось выше) будет достаточно хорошим лишь до тех пор, пока будут оставаться стабильными вероятностные характеристики «среды обитания» модели. Если же вероятностная структура среды изменится, модель начнет выдавать неверные прогнозы и будет лишь медленно приспосабливаться к новой среде.

Итак, вероятностный прогноз оказывается неточным как при слишком малом N («легкомысленная», «доверчивая» модель), так и при слишком большом N («косная», «скептическая» модель).

Рациональный выбор N зависит от того, в какой среде работает модель — как часто меняются вероятностные характеристики этой среды.

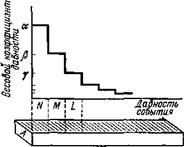
Рис. 10. Чем больше времени прошло после события, тем с меньшим весовым коэффициентом сохраняется в памяти след о нем

Таким образом, вероятность, с которой рассматриваемая система (опирающаяся на опыт последнего периода) прогнозирует событие В в случае наступления события Л, равна пв IN, где Пв — число карточек В среди первых N карточек в ящике А. Система подготавливается к действиям, соответствующим событиям А, В, С,..., в соответствии с величиной вероятностного прогноза па/N, Пв/N, nc/N, ...

Система будет работать гораздо лучше, если, в большей мере опираясь на опыт последнего периода, она вместе с тем не будет забывать и о событиях далекого прошлого. Пусть карточки в картотеке имеют некоторый «весовой коэффициент давности» события: лучше помнится то, что произошло недавно. Первые N карточек, стоящие в ящике (недавние события), имеют коэффициент а; следующие М карточек (более давние события) имеют коэффициент Р, меньший, чем а; дальнейшие а карточек (еще более давние события) — еще меньший коэффициент у и т. д. (рис. 10).