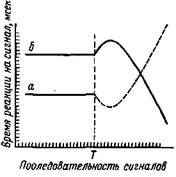
Рис. 4. Когда случайная последовательность сигналов А в Б сменяется повторением одного сигнала Б, время реакции на него сначала растет, а затем снижается

а — частый сигнал (А), б — редкий (Б), Г — момент изменения последовательности сигналов

Такой результат эксперимента хорошо согласуется с предположением, что время реакции зависит от вероятностного прогноза. По мере того как сигналы Б следовали подряд, оператор (испытуемый) со все большей вероятностью прогнозирует появление сигнала А. В соответствии с таким прогнозом время его реакции на сигнал Б растет, а на А уменьшается. Но когда число идущих подряд сигналов Б становилось достаточно большим, соотношение времени реакции на сигналы А и Б вновь изменялось: время реакции на Б снижалось, а на Л росло. Этс значит, что оператор уже перестал ждать сигнал А и прогнозирует новое появление сигнала Б — он изменил гипотезу о вероятностной структуре последовательности сигналов.

Однако описанных экспериментов еще недостаточно для утверждения, что скорость реакции при случайной последовательности сигналов является функцией вероятностного прогнозирования. Ведь в обеих сериях опытов экспериментатор переходил от случайной последовательности к жестко установленной. В одной серии (рис. 3) повторялась группа сигналов, в другой (рис. 4) — один сигнал. Для строгости доказательства необходимо было не только «развести» в эксперименте частоту сигналов и вероятностный прогноз их появления, но и до конца сохранить при этом случайную последовательность сигналов.

Отвечающий этим условиям эксперимент был задуман в следующей форме. Перед испытуемым четыре сигнала (назовем их А, Б, Б, Г), каждому из них соответствует кнопка, нажать которую надо при появлении сигнала. Существенной особенностью эксперимента была последовательность, в которой зажигались сигналы на пульте.

Рис. 5. Последовательность сигналов, группируемых в четверки

Первый сигнал выбирался случайным образом из четырех равновозможных. В случае, приведенном на рис. 5, это оказался сигнал Б. (Вероятность выбора для первого сигнала Pi=lU)- Следующий сигнал (на рис. 5 — В) выбирался из трех оставшихся с вероятностью Рп = Vs. Затем выбирался сигнал из двух оставшихся (на рисунке — Г) с вероятностью Риг = 'А. Наконец, следовал единственный оставшийся сигнал (в нашем примере — А), вероятность которого Р\у = 1. Таким образом, в пределах четверки сигналов вероятность появления каждого следующего сигнала увеличивалась.