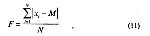Обработка данных. Для качественного анализа результатов опыта полезно построить гистограмму распределения подравниваний, что несложно сделать на компьютере с помощью практически любого статистического пакета. Кроме того целесообразно построить график распределения результатов подравниваний во времени. Наглядное представление результатов опыта в графической форме несомненно поможет глубже и содержательнее проанализировать не только различные стратегии решения испытуемым сенсорной задачи, но и наглядно оценить динамику его работы.

В качестве статистических мер, необходимых для оценки пороговых показателей, в МСО принято характеризовать полученное распределение чаще всего средним арифметическим (см. формулу (2) в предыдущем параграфе) и реже — медианой. В качестве мер разброса используются стандартное отклонение (см. формулу (3) в предыдущем параграфе) и реже — полумежквартальный размах. Очень редко в настоящее время используется такая мера изменчивости полученных данных, как среднее отклонение или средняя ошибка:

где xi — одно из значений в ряду подравниваний; М — среднее арифметическое подравниваний; n — количество подравниваний.

Меры чувствительности, используемые в МСО. В литературе можно найти разноречивые рекомендации в отношении мер чувствительности, которыми следует пользоваться в пороговых измерениях с помощью МСО. В результате экспериментов по подравниванию исследователь получает распределение установок испытуемого, которое характеризуется локализацией на стимульной оси и отмеченными выше показателями изменчивости. По мнению автора МСО Фехнера, при измерении этим методом исследователь получает не прямую оценку порога, а только пропорциональную ей величину, коей является один из показателей разброса — средняя ошибка. Логическим основанием для этого могло служить соображение о том, что в соответствии с инструкцией (подравнять переменный стимул к эталону) центр распределения подравниваний должен характеризовать субъективный эквивалент эталона. По смыслу введенных выше понятий он является точкой субъективного равенства .(PSE). Вместе с тем, чем более размыт, расплывчат субъективный эквивалент эталонного стимула, чем меньше испытуемый может отличить его от соседних значений, тем ниже чувствительность. По-видимому, Фехнер придавал именно такой психофизический смысл этому показателю разброса и поэтому описанный им метод был назван методом средней ошибки. Однако в целом ряде исследований были получены разные типы локализации распределения подравниваний на стимульной оси — смещенное и несмещенное относительно положения эталона. В связи с этим ряд исследователей (Челпанов, 1925; Осгуд, 1954; Торгерсон, 1958; Вудвортс и Шлосберг, 1965; Бардин, 1976) предлагают использовать в качестве меры чувствительности также и величину отстояния субъективного эквивалента эталона (центра распределения подравниваний) от эталона. Обосновывается это предложение тем, что чем ниже чувствительность испытуемого, тем более далекие стимулы он принимает равными эталону, поэтому эти два разные показателя как бы характеризуют чувствительность с разных сторон, и потому оба имеют право на существование. Вместе с тем никто из этих авторов не обращает внимания на то обстоятельство, что по смыслу введенных выше определений предлагаемая ими мера оценки чувствительности как разность значений точки субъективного равенства и эталона является константной ошибкой: СЕ = PSE - Sst.