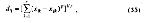§4. Построение метрической модели

В ходе построения пространственной модели данных необходимо измерять расстояния между точками-стимулами, чтобы соотносить их с исходными оценками различий. Для измерения расстояний в пространстве вводится метрика. Выбор метрики для психологического пространства также основывается скорее на содержательных аспектах данных, чем на формальных.

Так, Шепард (1964) предлагает условное деление стимулов на два класса в зависимости от их перцептивной целостности. Имеется в виду, что одни стимулы воспринимаются как целостные образования, и обычно сознательно не анализируются, например, цвета, запахи, фонемы и т.п., тогда как другие стимулы явно различаются по несвязанным между собой признакам, как, например, в работе Эттнива (1950), где стимулы — плоские геометрические фигуры — различались по величине, яркости и ориентации. В пространственной модели "не анализируемых" стимулов удобнее использовать евклидову метрику. Инвариантность евклидова расстояния относительно вращения систем координат (изотропность евклидова пространства) соответствует в данном случае такому типу поведения испытуемого, как если бы он оценивал различия между простыми, одномерными объектами. В случае явно "анализируемых" стимулов, когда итоговая оценка составляется как бы из последовательного добавления по очередному признаку, более подходит "sity-block"-метрика.

И метрика "sky-block", и евклидова метрика являются частными случаями одной общей функции:

известной как метрика Минковского. Для случая "sity-block" р = 1, а для евклидовой метрики — р = 2.

Конечно, выбор метрики определяется не только тем, "анализируемые" стимулы или "не анализируемые", и не ограничивается двумя приведенными видами метрик. В некоторых работах предлагается решать задачу для нескольких значений р, и затем экспериментатор выбирает наиболее "интерпретируемую" модель расстояния. Например, для пространственной модели цветоразличения Крускел (1964), варьируя в выражении (35) показатель р от 1 до 5, получил, что в данном случае наиболее подходит метрика с р=2.5. В другой работе (Шепард, 1962) было показано, что в пространстве цветоразличения можно принять евклидову метрику, если использовать нелинейную форму соотношения между исходными мерами сходства и межточечными расстояниями.