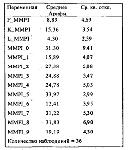
§4. Дополнительные статистические показатели для оценки результатов факторного анализа

В начале предыдущего параграфа мы отмечали, что вычислительные алгоритмы ФА основываются на ряде математических допущений о характере эмпирических данных, подвергаемых ФА. Остановимся на ряде статистических показателей, которые помогают исследователю оценить степень соответствия данных этим допущениям.

Как правило, в любой программе по ФА предусмотрен расчет показателей описательной статистики по матрице смешения. Например в статистических системах "Stadia" и SPSS для каждой переменной вычисляются общее количество наблюдений, среднее арифметическое значение и среднее квадратичное отклонение (см. табл. 3). Эти достаточно простые показатели позволяют быстро сравнить между собой все анализируемые переменные, и уже на уровне анализа исходных данных попытаться найти возможные ошибки, связанные либо с проведенными измерениями, либо с вводом данных в компьютер. Например, если при сборе данных использовалась 7-балльная шкала, то наверное вас насторожит среднее значение по какой-то переменной, равное 0.87, или резко отличающаяся от других величина среднего квадратичного отклонения.

Таблица 3. Данные описательной статистики для 9 переменных

Коэффициент сферичности Бартлета используется для оценки "хорошести" корреляционной матрицы. Если этот коэффициент достаточно большой, а соответствующий ему уровень значимости мал (например, меньше 0.05 или 0.01), то это свидетельствует о надежности вычисления корреляционной матрицы. При высоком уровне значимости исследователю стоит задуматься об адекватности использования ФА с полученными данными.

Кроме того, для оценки надежности вычислений элементов корреляционной матрицы и возможности ее описания с помощью ФА во многих статистических программах применяется так называемая мера адекватности выборки Кайзера—Мейера—Олкина(КМО) (СНОСКА: Имеется в виду адекватность факторной модели данному набору переменных, описываемому корреляционной матрицей). По мнению Г. Кайзера (1974), значения КМО около 0.9 оцениваются как "изумительные", 0.8 — "достойные похвалы", 0.7 — "средние", 0.6 — "посредственные", 0.5 — "плохие", а ниже 0.5 — "неприемлемые". Для оценки надежности вклада в корреляционную матрицу каждой переменной в отдельности также используют меру выборочной адекватности (например, коэффициент MSA в системе SPSS). Вышеприведенные характеристики Г. Кайзера вполне справедливы и для оценки этих величин тоже. Исследование надежности каждой переменной позволяет исключить из расчетов одну или несколько переменных, и тем самым повысить результативность ФА.