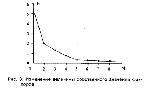
Таблица 2. Статистические показатели для определения минимального количества факторов

Первый важный показатель в этой таблице (второй столбец) — это величина собственного значения каждого фактора; факторы расположены в таблице по убыванию этой величины. Не очень строго говоря, этот показатель характеризует вес, значимость каждого фактора в найденном факторном решении (СНОСКА: Более точно, собственное значение каждого фактора — это его вклад в дисперсию переменных, объясняемую влиянием общих факторов. Расчет собственных значений корреляционной матрицы — один из основных вычислительных алгоритмов ФА). Из таблицы 2 видно, что от 1-го фактора к 10-му (всего было 10 переменных) величина собственного значения убывает более, чем в 100 раз. Естественно возникает вопрос о том, какая величина данного показателя свидетельствует о значимом, существенном вкладе соответствующего фактора, и каков критерий для отсечения незначимых, несущественных факторов. Достаточно часто в качестве такого критического значения используют величину собственного значения, равную 1.0. Таким образом, с определенной степенью уверенности предполагают, что те факторы, у которых этот показатель меньше 1.0, не вносят значительного вклада в объяснение корреляционной матрицы. Кроме анализа табличных величин бывает полезно визуально оценить динамику величины собственного значения по графику. Как правило, в большинстве статистических программ такая возможность пользователю предоставляется (см. рис. 3). Как предлагал в свое время Р. Кеттел (1965), выделение факторов заканчивается, когда после резкого падения величины собственного значения изменяются незначительно, и график фактически превращается в горизонтальную прямую линию. Несмотря на видимую простоту и ясность такого рецепта, следует отметить, что когда на графике имеется более чем один излом, то выделение горизонтального участка становится неоднозначным.

Другой не менее важный расчетный показатель значимости каждого фактора — процент объясняемой дисперсии переменных, содержащейся в корреляционной матрице (третий столбец в табл. 2). Естественно, что все 100% дисперсии будут объясняться только всеми десятью факторами. Однако не стоит забывать, что при любых измерениях (а особенно в разведочных, пилотажных исследованиях) имеют место разного рода случайные ошибки, и поэтому их вклад в общую дисперсию тоже может оказаться весьма значительным. Предполагается, что ряд выделенных факторов отражает влияние случайных процессов, никак не связанных с оценкой наблюдаемых переменных. Таким образом, формально задача заключается в том, чтобы, с одной стороны, выбрать некоторое минимальное количество факторов, которые бы, с другой стороны, объясняли достаточно большой процент всей дисперсии переменных. Ясно, что эти два требования в принципе взаимно противоречивы, и, следовательно, исследователь стоит перед выбором некоторой критической величины процента объясняемой дисперсии. К сожалению, никаких строго формальных рецептов по этому поводу не существует, но принято считать, что при хорошем факторном решении выбирают столько факторов, чтобы они в сумме (последний столбец таблицы) объясняли не менее 70—75%. В хорошо спланированных исследованиях с установленной факторной структурой этот суммарный процент может достигать 85—90 %.