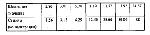
9. Так как оценки могут сильно отклоняться от оценок "среднего" наблюдателя, то желательно использовать группу наблюдателей, которая достаточно велика, чтобы получить при обработке устойчивую медиану.

В методе оценки величин шкальные значения измеряемого субъектом признака содержатся в ответах испытуемых и могут быть представлены медианой или геометрическим средним всех оценок группы испытуемых, относящихся к каждому из стимулов. Медиана является более грубой, чем геометрическое среднее, мерой центральной тенденции. Геометрическое среднее в отличие от среднего арифметического логически более обосновано, т.к. в результате измерения обычно получается нелинейная психофизическая функция типа R = aYn. Геометрическое среднее определяется равенством (1). При большом числе измерений рекомендуется логарифмический вариант равенства (2).

Рассмотрим пример из упомянутой выше работы Энгена (1971), в которой каждый из испытуемых дважды оценивал 7 различных концентраций запаха амилацетата, разведенного в диэтилфтолате. В качестве модуля, которому приписывалось значение 10, предъявлялась концентрация 12.5°. Геометрические средние оценок представлены в табл.2.

Представление этих данных в линейных координатах показывает, что полученная психофизическая функция нелинейна и характеризуется замедляющимся ускорением: только при малых концентрациях амилацетата прирост запаха опережает рост концентрации. Будучи представлена в двойных логарифмических координатах, эта функция хорошо аппроксимируется прямой с наклоном <1. Следовательно, полученная психофизическая зависимость относится к числу степенных функций с показателем степени <1.

Таблица 2. Субъективная шкале запаха амилацетата, разведенного в диэтилфтолате

Наиболее существенным недостатком метода оценки величин с заданным модулем может быть зависимость экспоненты степенной функции от места заданного модуля в стимульном ряду. Наличие такой зависимости (Энген, 1971) весьма неприятно тем, что ставит под сомнение экспоненту степенной функции как специальную характеристику модальности стимульного континуума. Однако существование такой зависимости далеко не всегда подтверждается экспериментами (Стивенc, 1956; Джонс и Восков, 1966).