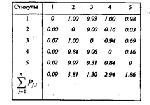
Примечания: элементом матрицы рi,j является вероятность, с которой стимул i в nape j,i оценивался более предпочтительным, чем стимул j.

Преобразуем вероятности рi,j в единицы стандартного отклонения нормального распределения — zi,j.

Таблица 5. Матрица Z — оценок

Примечания: элементом матрицы Zi,j является вероятность рj,i, преобразованная в единицы стандартного отклонения.

Таблица 6. Матрица Z' — оценок

Примечания: элементом матрицы Zi,j является вероятность р'j,i преобразованная в единицы стандартного отклонения. Столбцы упорядочены по возрастанию ∑ p'j,i .

Переставим столбцы в матрице Z в таком порядке, чтобы первый столбец имел наименьшую сумму элементов, а последний — наибольшую.

Таблица 7. Матрица разностей между столбцами

Из матрицы Z' можно получить матрицу различий между соседними парами столбцов, вычитая их поэлементно один из другого. В каждой j-й строке элемент этой матрицы будет равен (zj,i+1 - zj,i).

Пользуясь выражением (20), вычисляем из полученных различий шкальные значения стимулов, приняв, что S1 = 0:

S1 = 0,

S3 = 0 + 1.5 = 1.5,

S5 = 1.5 + 0.53 = 2.03,

S4 = 2.03 + 0.98 = 3.01,

S2 = 3.01 + 0.56 = 3.97.

Из рассмотренной процедуры видно, что недостающие элементы матрицы компенсируются наличием внутренней связи между элементами столбца, что позволяет рассматривать разность между столбцами матрицы как результат алгебраической интерполяции отсутствующих элементов в столбце.