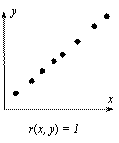
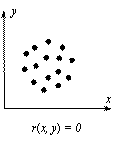
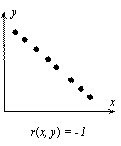
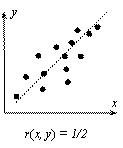
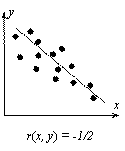
Корреляционный анализ. Корреляция (Correlation) – связь между двумя или более переменными (в последнем случае корреляция называется множественной). Цель корреляционного анализа – установление наличия или отсутствия этой связи, то есть установление факта зависимости каких-либо явлений, процессов друг от друга или их независимости.

В случае, когда имеются две переменные, значения которых измерены в шкале отношений (СНОСКА: Единицы измерений при этом не важны – например, масса тела может быть измерена в граммах, килограммах, тоннах – они не влияют на значение коэффициента корреляции), используется коэффициент линейной корреляции Пирсона r, который принимает значения от -1 до +1 (нулевое его значение свидетельствует об отсутствии корреляции (СНОСКА: Корректно говоря, этот факт справедлив в случае, если анализируемая пара переменных описывается двумерным нормальным распределением (см. подробности, например, в [183]))) – см.

Рис. 12, на котором каждая точка соответствует отдельному объекту, описываемому двумя переменным – x и y. Термин «линейный» свидетельствует о том, что исследуется наличие линейной связи между переменными – если r(x, y) = 1, то одна переменная линейно зависит от другой (и, естественно, наоборот), то есть существуют константы a и b, причем a > 0, такие что y = a x + b.

На

Рис. 12а) и в) изображены ситуации, когда все экспериментальные точки лежат на прямой (абсолютное значение коэффициента линейной корреляции равно единице). В ситуации, изображенной на рисунке

Рис. 12б), однозначно провести прямую через экспериментальные точки невозможно (коэффициент линейной корреляции равен нулю).

а)	б)		в)
г)		д)