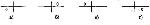1.        Он равен единице либо когда с = 0 /схема 3.4.1 а)/, либо d = 0 /схема 3.4.1 б)/. В первом случае все «не политологи» относятся к «остальным» по удовлетворенности. Обратное утверждение неверно. Во втором случае все политологи удовлетворены учебой на 4 балла. Опять же обратное утверждение будет неверным.

2.        Он равен минус единице, если а = 0 /схема 3.4.1 в)/ или b = 0 /схема 3.4.1 г)/. В первом случае все политологи относятся к «остальным» по удовлетворенности. Во втором случае все «не политологи» удовлетворены учебой на четыре балла. Обратные утверждения неверны.

Схема 3.4.1

3.        Коэффициент равен нулю, если ab = cd, т. е. в случае статистической независимости наших изучаемых свойств.

В нашем случае коэффициент равен 0,14. Естественным образом, возникает вопрос, каким будет значение коэффициента для генеральной совокупности. Ведь пока мы получили только оценку связи по выборочной совокупности. Значение коэффициента небольшое, но отличное от нуля, поэтому возникает другой вопрос. Значимо ли это отличие от нуля или мы получили ненулевое значение случайно? Если это отклонение незначимо, то наблюдается статистическая независимость наших свойств (быть политологом и быть удовлетворенным учебой на четыре балла). И наоборот, если это отклонение значимо, то имеем случай статистической зависимости. Для определения значимости и для определения «истинного» значения (для генеральной совокупности) необходим аппарат математической статистики, а именно аппарат проверки статистических гипотез. Их не следует путать с содержательными гипотезами исследования. К этому вопросу мы вернемся несколько позже после введения так называемой статистики хи-квадрат.

Рассмотрим использование меры Юла в сравнительном контексте. Пусть целевое свойство ¾ «быть удовлетворенным учебой на четыре балла». Попытаемся определить, какая из будущих профессий теснее связана с этим свойством, сильнее влияет на подобную удовлетворенность. По данным, представленным в таблице 3.3.1, сформируем таблицы сопряженности вида (2x2) для подсчета шести значений для шести будущих профессий. Так как для политологов значение коэффициента уже было получено по таблице 3.4.1, то ниже на схеме 3.4.2 приведены таблицы для оставшихся пяти будущих профессий. В этих таблицах приведены только абсолютные частоты. Целевой признак обозначен как (У). (+У) и означает обладать свойством «удовлетворенности учебой четыре балла», а (-У) ¾ не обладать, т. е. остальные варианты удовлетворенности учебой.