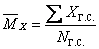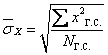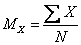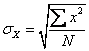| § | библиотека – мастерская – | Помощь Контакты | Вход — |
Готтсданкер Р. Основы психологического эксперимента: Учеб. пособие. Пер. с англ. —— М.: Изд-во Моск. ун-та, 1982. — 464 с.
Стр. 73 Поскольку
То
Оценка стандартного отклонения генеральной совокупности Для определения среднего генеральной совокупности, которое могло бы быть получено в бесконечном эксперименте, наилучшей оценкой фактически было среднее по выборке. Иначе обстоит дело со стандартным отклонением. В любом наборе реальных проб имеет место меньшее число результатов с очень высокими или очень низкими значениями, чем в генеральной совокупности. А поскольку стандартное отклонение является мерой разброса оценок, то его величина, определенная на основе выборки, всегда меньше параметра генеральной совокупности сигма σх. Более точная, оценка стандартного отклонения для генеральной совокупности находится по формуле
Или
Для наших числовых данных:
В некоторых экспериментах высказывается гипотеза, что поведение в одном условии более вариативно, чем в другом. Тогда целесообразнее сравнивать стандартные отклонения, а не средние. Если для обоих условий N одно и то же, можно сравнивать между собой сигмы. Однако когда N различны, сигма для условия с меньшим N дает более заниженную оценку такого параметра генеральной совокупности, как стандартное отклонение. Поэтому следует сравнивать два S. Таблица, которая приводится ниже, поможет вам запомнить эти положения и формулы.
|
Реклама
|
||||||||||||||||||||||
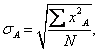
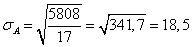 мс.
мс.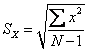 (2.2)
(2.2)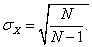 (2.2А)
(2.2А)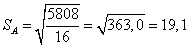 мс.
мс.