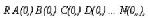Главные артефакты этого плана — кумуляция эффектов последовательности и тестирования. Кроме того, искажающее влияние на результаты может оказывать временной фактор (эффект естественного развития).

Схема этого плана выглядит очень просто: АО, ВОд, где А и В — разные условия. Испытуемые могут отбираться из генеральной популяции случайным образом или представлять собой естественную группу.

Обработка данных сводится к оценка сходства между результатами тестирования в условиях А и В. Для контроля эффекта последовательности можно произвести контрбалансировку и перейти к корреляционному плану для двух групп:

В этом случае мы можем рассматривать А и В как воздействия, а план — как квазиэксперимент.

3.     Корреляционное исследование попарно эквивалентных групп.

Этот план используется при исследовании близнецов методом внутрипар-ных корреляций. Дизиготные или монозиготные близнецы разбиваются на две группы: в каждой — один близнец из пары. У близнецов обеих групп измеряют интересующие исследователя психические параметры. Затем вычисляется корреляция между параметрами (0-корреляция) или близнецами (Р-корреляция). Существует множество более сложных вариантов планов психогенетических исследований близнецов.

4.     Для проверки гипотезы о статистической связи нескольких переменных, характеризующих поведение, проводится структурное корреляционное исследование. Оно реализуется по следующей программе. Отбирается группа, которая представляет либо генеральную совокупность, либо интересующую нас популяцию. Отбираются тесты, проверенные на надежность и внутреннюю валидность. Затем групп а тестируется по определенной программе:

Где А, В, С ... N — тесты.

Данные исследования представлены в форме матрицы: тх п, где т — количество испытуемых, n — тесты. Матрица "сырых" данных обрабатывается, подсчитываются коэффициенты линейной корреляции. Получается матрица вида тх n, где n — число тестов. В клеточках матрицы — коэффициенты корреляции, по ее диагонали — единицы (корреляция теста с самим собой). Матрица симметрична относительно этой диагонали. Корреляции оцениваются на статистические различия следующим образом: сначала г переводится в Z-оценки, затем для сравнения г применяется t-критерий Стьюдента. Значимость корреляции оценивается при ее сопоставлении с табличным значением. При сравнении ,, и r принимается гипотеза о значимом отличии корреляции от случайной при заданном значении точности ( а = 0,05 или а = 0,001). В некоторых случаях возникает необходимость вычисления множественных корреляций, частных корреляций, корреляционных отношений или редукции размерности — уменьшения числа параметров.