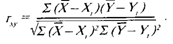Нулевой называется корреляция при отсутствии связи переменных.

В психологии практически нет примеров строго линейных связей (положительных или отрицательных). Большинство связей — нелинейные. Классический пример нелинейной зависимости — закон Йеркса — Додсона:. возрастание мотивации первоначально повышает эффективность научения, а затем наступает снижение продуктивности (эффект "перемотивации"). Другим примером является связь между уровнем мотивации достижений и выбором задач различной трудности. Лица, мотивированные надеждой на успех, предпочитают задания среднего диапазона трудности — частота выборов на шкале трудности описывается колоколообразной кривой.

Математическую теорию линейных корреляций разработал Пирсон. Ее основания и приложения излагаются в соответствующих учебниках и справочниках по математической статистике. Напомним, что коэффициент линейной корреляции Пирсона г варьируется от -1 до +1. Он вычисляется путем нормирования ковариации переменных на произведение их среднеквадратических отклонений.

Значимость коэффициента корреляции зависит от принятого уровня значимости а и от величины выборки. Чем больше модуль коэффициента корреляции, тем ближе связь переменных к линейной функциональной зависимости.

Планирование корреляционного исследования

План корреляционного исследования является разновидностью квазиэкспериментального плана при отсутствии воздействия независимой переменной на зависимые. В более строгом смысле: тестируемые группы должны быть в эквивалентных неизменных условиях. При корреляционном исследовании все измеряемые переменные — зависимые. Фактором, определяющим эту зависимость, может быть одна из переменных или скрытая, не измеряемая переменная.

Корреляционное исследование разбивается на серию независимых друг от друга измерений в группе испытуемых Р. Различают простое и сравнительное корреляционные исследования. В первом случае группа испытуемых однородна. Во втором случае мы имеем несколько рандомизированных групп, различающихся по одному или нескольким определенным критериям. В общем виде план такого исследования описывается матрицей вида: Рх О (испытуемые х измерения). Результатом его является матрица корреляций. Обработку данных можно вести, сравнивая строки исходной матрицы или столбцы. Коррелируя между собой строки, мы сопоставляем друг с другом испытуемых; корреляции же интерпретируются как коэффициенты сходства — различия людей между собой. Разумеется, Р-корреляции можно вычислять лишь в том случае, если данные приведены к одной шкальной размерности, в частности, с помощью Z-