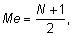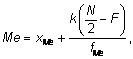Медиана, или центральная величина ряда,– это величина члена, приходящего на середину ранжированного ряда, при нечетном числе членов ранжированного ряда медиана соответствует центральной величине ряда. Например, мы имеем следующий ранжированный ряд: 4, 5, 7, 9, 11, 13, 15, 17, 18. В середине данного ряда находится число 11, следовательно, оно и является медианой.

Порядковый номер медианы вычисляется по формуле:

где N – число членов в ряду.

Медиана в интервальном ряду вычисляется по формуле:

Где xMe – значение нижней границы медианного интервала;

k – длина медианного интервала;

N – число членов совокупности (åfi при сумме малых частот N = åfi + 1);

fMe – частота медианного интервала.

Для больших совокупностей данных, где есть объединенные классы, медиана находится следующим образом (смотри таблицу 8). Пусть мы имеем 16 оценок:

Таблица 8

Таблица оценок

= 16

Медиана выбирается 8-й и 9-й оценками. По таблице 8 видно, что она располагается в интервале четверок. Поскольку в верхней границе ряда оценок накоплено 4 оценки (1 + 3 = 4), мы должны еще накопить 8 - 4 = 4 частоты, а всего в интервале 8 четверок. Поэтому медиана делит интервал четверок пополам. В интервале между значениями 3,5 и 4,5 лежит 8 четверок. Следовательно, медиана равна 3,5 + 4:8 = 4.

Интерпретируем значение медианы на следующем примере. Пусть мы получили следующий ряд оценок 2, 2, 3, 4, 5, 5, 5, где медиана равна оценке 4. Разность между 4 и 2 составляет два, между 4 и 5 минус один. Сумма этих разностей, взятых по абсолютному значению (т.е. без знака), равна 2+2+1+1+1+1 = 8 и всегда меньше суммы разностей относительно любого другого числа данного ряда. В самом деле разности между 5 и другими числами соответственно равны 3, 3, 2, 1, 0, 0, а их сумма абсолютных разностей всех значений относительно медианы всегда меньше суммы разностей относительно любой другой точки. Из этого следует, что если вместо каждой оценки ряда выбрать медиану, то будет допущена минимальная суммарная ошибка.